Представьте, что вы хотите провести опрос: например, выяснить, сколько людей поддерживают новую инициативу в городе. Очевидно, опросить всех жителей невозможно — это слишком долго и дорого. Поэтому учёные и аналитики используют выборку — часть всей совокупности. Но чтобы результаты были достоверными, важно правильно рассчитать её размер.
Почему размер выборки имеет значение
Слишком маленькая выборка может дать искажённые результаты: мнения пары десятков человек вряд ли отражают позицию всего города. Слишком большая — наоборот, потребует лишних затрат времени и ресурсов. Баланс достигается с помощью статистики.
Основные параметры расчёта
При определении размера выборки учитываются:
- Уровень доверия — вероятность того, что результаты верны для всей совокупности (обычно 95%).
- Допустимая погрешность — насколько можно ошибиться (например, ±5%).
- Доля признака в совокупности — предварительная оценка того, сколько людей могут выбрать тот или иной вариант. Если информации нет, берут 50% для «худшего случая».
- Объём генеральной совокупности — общее число людей или объектов, среди которых проводится исследование.
Базовая формула
Для больших совокупностей часто используют упрощённую формулу:
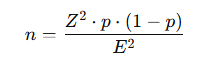
Где:
- n — размер выборки,
- Z — значение для выбранного уровня доверия (для 95% ≈ 1,96),
- p — предполагаемая доля признака,
- E — допустимая ошибка (например, 0,05 для 5%).
Пример
Допустим, вы хотите узнать мнение горожан о новом парке.
- Уровень доверия: 95%
- Погрешность: 5%
- Предположим, половина поддерживает инициативу (p = 0,5).
Подставим:
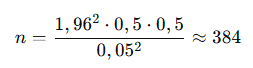
То есть достаточно опросить около 400 человек, чтобы с высокой вероятностью получить надёжный результат.
Важные нюансы
- Если ваша генеральная совокупность очень маленькая (например, 200 человек), формула корректируется специальным коэффициентом.
- При меньшей погрешности (например, 3%) размер выборки быстро растёт.
- Онлайн-калькуляторы упрощают расчёт — достаточно ввести параметры.
✅ Итог: правильно рассчитанная выборка позволяет сэкономить ресурсы и при этом получить результаты, на которые можно опираться в исследованиях и принятии решений.

